Законы пропорций и оптических иллюзий в архитектуре Египта
ЗАКОНЫ ПРОПОРЦИЙ И ОПТИЧЕСКИХ ИЛЛЮЗИЙ
ПРОПОРЦИИ
Чем достигается пропорциональность? Создается ли она инстинктивным чувством гармонии или является результатом основанного на определенном методе графического построения? Сравнивая отдельные части египетских зданий, обычно можно установить между их размерами самые простые отношения, например 1 : 2 или 3 : 5. И почти всегда эти отношения можно выразить общей мерой в целых числах.
При кладке здания из кирпича такой единицей измерения является кирпич. Кирпичи изготовляются одного размера и, чтобы использовать их целиком, не обсекая, размеры здания должны быть взяты в кратном отношении к размерам кирпича. Таким образом, кирпич является общей единицей измерения или естественным «модулем».
В конструкциях из тесаного камня приходится считаться с такой же, хотя, быть может, менее настоятельной, необходимостью выражать размеры в целых числах. Только при этом условии можно обеспечить правильный и непрерывный ход работ. Египтяне имели разработанную систему мер. Инстинкт и практический опыт заставили их подчинять все размеры единому модулю. Такая единица измерения является обязательным модулем для всех частей здания. С появлением понятия меры и пропорции всего естественнее было остановиться на простейших из них, из которых неизбежно вытекает закон простых отношений.
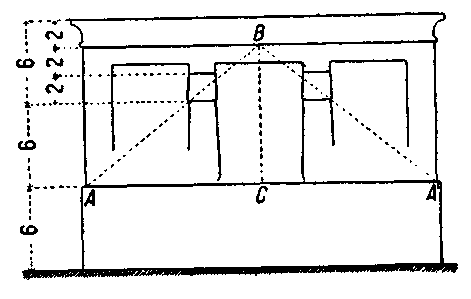
Арифметические отношения. — Рисунок 36 показывает применение простых отношений в египетских памятниках. Здесь дан чертеж Элефантинского храма. Обмер произведен архитекторами, сопровождавшими египетскую экспедицию Наполеона.
Установлены следующие соотношения отдельных частей здания.
Общая высота здания делится на три равные части:
1. Цоколь.
2. Ствол колонны.
3. Верхняя часть здания до основания капители.
Последняя часть делится в свою очередь также на три части:
1. Капитель.
2. Абака и архитрав.
3. Карниз.
Каждое подразделение выражается целым числом в единице меры, равняющейся одному египетскому футу (36 см), и точно соответствует двум таким футам. Мы находим здесь одновременно простые отношения и целые числа; в этом — вся сущность пропорций.
 |
 |
| Рис. 36 | Рис. 37 |
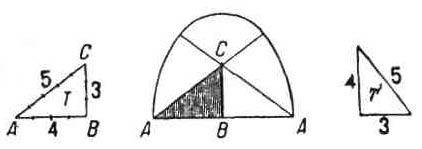
Геометрические отношения. — Но египтяне не ограничивались арифметическими отношениями. Их склонности к геометризму отвечали изящные геометрические построения. Известно древнее решение задачи прямоугольного треугольника, где прямой угол определяется при помощи треугольника, стороны которого относятся друг к другу, как 3:4:5. Плутарх сообщает, что этот треугольник с соизмеримыми сторонами считался египтянами священным, и они часто пользовались им. Так, при начертании сводов они поступали следующим образом (рисунок 37):
Кривая сводов описывалась циркулем из трех центров, взятых в точках А, Си А двух египетских треугольников. При разработке проектов зданий это вело к установлению таких пропорций, при которых в контуры здания мог быть вписан указанный треугольник. Из этих треугольников, служивших для установления пропорций, обычно пользовались лишь треугольниками с соизмеримыми сторонами в отношении 3:4:5 (треугольник Т или Т, рисунок 37) или треугольниками рисунка 38, которые составляются из сочетания в ином порядке сторон, выраженных числами 3,4 и 5.
В Элефантинском храме в основу пропорций положен треугольник R (рисунок 38). На чертеже рисунка 36 изображено, каким образом он вписывается в контур фасада.
Кроме треугольников, берущих свое начало от египетских треугольников со сторонами 3, 4 и 5, встречаются другие треугольники, изображенные на рисунке 39 буквами E,G и М.
Е — равносторонний треугольник;
G — треугольник, полученный путем сечения по диагональной плоскости пирамиды Хеопса, профиль которой — равносторонний треугольник;
М— треугольник, высота которого получается делением основания в крайнем и среднем отношении.
На первый взгляд применение этих треугольников противоречит принципу модуля и простых отношений. Перед нами как будто два взаимно исключающих друг друга метода построения, один — посредством чисел, другой — посредством треугольников.
|
|
|
Рис. 38 |
|
|
|
Рис. 39 |
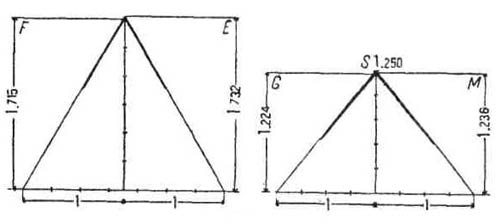
Согласование арифметического и графического методов. — Интересно отметить, что фактически метод треугольников и метод модульных отношений дают почти совпадающие результаты и что в пределах обычных приближений применение треугольников дает простые отношения размеров, иначе говоря, оба метода сливаются в один. Эти наблюдения сделаны Бабеном. Рисунок 39 наглядно показывает совпадение результатов обоих методов.
В группе Е, F мы накладываем на равносторонний треугольник другой треугольник, у которого высота равна 6/7 основания. Контуры их почти совпадают. По сторонам можно вычислить величину отклонения. Треугольник с отношением высоты к основанию, равным 7 : 8, почти не отличается от равностороннего.
В группе G, S, M (S — производный от египетского треугольника со сторонами 3, 4 и 5) при наложении усматривается такое же совпадение. Следовательно, оба метода, несмотря на то, что их часто противопоставляли друг другу, дают одинаковые результаты. Нужна исключительная точность постройки и точнейшие способы измерения ее частей, чтобы установить, что именно было положено в ее основу — арифметический ли расчет или геометрические комбинации треугольников. При построении равностороннего треугольника или треугольника, высота которого равна 6/7 основания, линии их совпадают.
При разделении прямой в среднем и крайнем отношении, или при разделении ее на две части с отношением 5 : 3 фактически получается одно и то же. Отношения 5 : 3 и 6 :7 согласуют простые арифметические отношения с замечательными геометрическими свойствами. Частое повторение пропорций, совпадающих с начертанием треугольников, данных на рисунке 39, позволяет думать, что этими треугольниками действительно руководились при постройках. Положение можно резюмировать следующим образом.
Египтяне придерживались модульных пропорций и простых отношений; из простых отношений они предпочтительно пользовались такими, которые совпадают с геометрическими построениями. Впечатление гармонии усиливается выбором таких модульных пропорций, которые отвечают понятию изящного.
Практическое значение метода. — С точки зрения практического строительства арифметические отношения и построения, полученные посредством треугольников, поддаются наглядному изображению, которое позволяет зодчему без помощи письма передать свой замысел, установить правила и создать школу.
С точки зрения гармонии форм значение метода еще важнее. Идея единства в произведении искусства есть основной закон создания ансамбля. Мы чувствуем сущность и значение этого закона, еще не осознавая его. Дисгармония в музыке, ложно прочувствованные пропорции в архитектуре оскорбляют наше эстетическое чувство, заложенное в человеческой природе. Зодчеству нужна определенная закономерность, и безразлично, в чем она находит свое выражение — в геометрии или в числах.
Из всех остальных законов закон простых отношений кажется наиболее обязательным. Он распространяется не на одну только архитектуру. В музыке ему подчиняется число колебаний, в мелодии — это такт, в стихе — ритм. Древнейшее зодчество ритмично, и этим сразу определяются и его принцип и система применения. Египтяне, а вслед за ними и греки, достигали гармонии модульными комбинациями. Следует ли из этого, что и нам надо идти этим путем? Отнюдь нет. Ведь мы не подчиняем нашу живую речь закону древней просодии. Но там, где этот ритм был соблюден, он пробуждает в нас идею гармонии, рождающую чувство красоты.
СИММЕТРИЯ, РИТМИЧЕСКОЕ ПОВТОРЕНИЕ, ОПТИЧЕСКИЕ ИЛЛЮЗИИ
Египетское искусство достигает особой выразительности приемом ритмических повторений. Анфилады колонн, сдвоенные ряды сфинксов, одинаковость поз в статуях усиливают впечатление архитектурного комплекса.
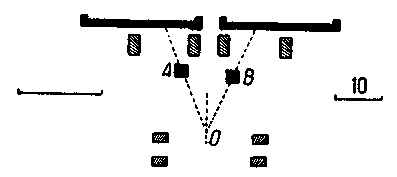
Симметрия — господствующая особенность египетского искусства. Ни одна архитектура не уравновешивает так массы, как египетская. Нигде не умели так использовать естественные условия для достижения определенного впечатления. Луксорский храм представляет ряд дворов, имеющих форму неправильных прямоугольников. Египетским зодчим было известно, что глаз неверно воспринимает углы плана, и потому они допускали некоторые неправильности, ускользающие от зрителя. Обелиски А и В (рисунок 40), стоявшие когда-то перед входом в храм, были различной величины. Для того чтобы создать иллюзию двух обелисков одинаковой высоты, меньший из них В был выдвинут на передний план. Впечатление глубины во дворе Рамессеума усиливается благодаря постепенному уменьшению колонны по мере их удаления, для чего воспользовались подъемом почвы. В настоящее время этот прием обычно применяется в театральных декорациях.
|
|
|
Рис. 40 |
|
|
|
Рис. 41 |
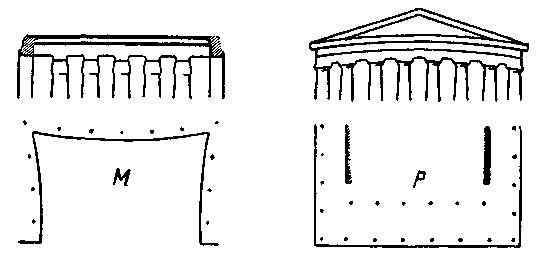
Умение египтян использовать законы оптических иллюзий превзошли только греки. Как доказал Паннеторн, египтянам был известен странный обман зрения, получающийся при восприятии длиной горизонтальной линии. Так, например, линия архитрава кажется провисшей посредине. Греки боролись с этой оптической иллюзией, придавая архитраву выгиб в направлении, противоположном кажущемуся искривлению (рисунок 41, Р). В храме Мединет Абу нет этого выгиба, но архитрав в плане представляет кривую, показанную на рисунке 41, М. Перспективный эффект тот же. В обоих случаях кривизна эта едва заметна. На чертежах же она для большей наглядности сильно подчеркнута.
Намеренные изменения точных геометрических линий, нюансировку, возможную только в утонченном, вполне овладевшем своими методами искусстве, мы будем рассматривать в связи с греческой архитектурой.
Укажем здесь лишь на общность тенденций и на глубокий анализ законов оптического восприятия в египетском зодчестве, которое на тысячу лет опередило в этом отношении греческое искусство.
Огюст Шуази. История архитектуры. Auguste Choisy. Histoire De L'Architecture

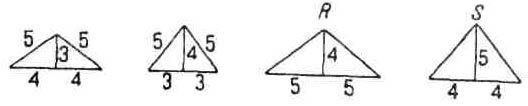

Добавить комментарий